The How To Write A Polynomial Function With Given Zeros article we provide is expected to provide useful information for you, all of which we have summarized well.

Writing Polynomial Functions with Given Zeros: A Comprehensive Guide

I remember vividly the moment I realized the beauty of polynomial functions. It was during a high school algebra class, where our teacher asked us to write a function with a specific set of zeros. The concept seemed daunting at first, but as I delved deeper, I was amazed by the power and elegance behind this mathematical tool. In this article, we will embark on a comprehensive journey, exploring the intricacies of writing polynomial functions with given zeros.

Polynomial Functions: A Definition

A polynomial function is a mathematical expression that represents a sum of terms, each consisting of a constant multiplied by a variable raised to a non-negative integer power. The degree of a polynomial function is the highest power to which the variable is raised. Polynomial functions are widely used in various fields, from engineering and physics to economics and finance.

Finding Polynomial Functions with Given Zeros

To write a polynomial function with given zeros, we employ a technique known as the Factor Theorem. This states that if a polynomial function f(x) has a zero at x = a, then (x – a) is a factor of f(x).

Understanding the Factor Theorem

The Factor Theorem arises from the fundamental concept of polynomial division. When we divide a polynomial f(x) by (x – a), the remainder is f(a). Therefore, if f(a) = 0, then (x – a) divides f(x) without leaving a remainder. This implies that (x – a) is a factor of f(x).

Steps for Writing Polynomial Functions with Given Zeros

To write a polynomial function with a given set of zeros, follow these steps:

1. Factor the Polynomial: If the zeros are given as single values, factor the polynomial by multiplying together the factors (x – a), where a represents each zero. For complex zeros, use (x – a)(x – ā), where ā denotes the complex conjugate of a.
2. Multiply the Factors: Expand the multiplication of the factored terms to obtain the polynomial function.
3. Simplify (Optional): Combine like terms and simplify the polynomial if possible.

Example: Finding a Polynomial with Zeros of 2, -1, and 3

Suppose we want to find a polynomial function with zeros at x = 2, x = -1, and x = 3.

Step 1: Factor the Polynomial
(x – 2)(x + 1)(x – 3)

Step 2: Multiply the Factors
(x – 2)(x + 1)(x – 3)
= (x^2 – x – 2x + 2)(x – 3)
= (x^2 – 3x + 2)(x – 3)
= x^3 – 3x^2 + 2x – 3x^2 + 9x – 6

Step 3: Simplify
f(x) = x^3 – 6x^2 + 11x – 6

Tips and Expert Advice

• Start with Small Sets of Zeros: Begin with polynomials with a small number of zeros to build a strong foundation.
• Practice Factoring Polynomials: The ability to factor polynomials is crucial for writing functions with given zeros.
• Use Synthetic Division: This technique can simplify polynomial division, especially when dealing with complex zeros.
• Seek Additional Resources: Consult textbooks, online tutorials, and math forums for further guidance.

Explaining the Tips and Expert Advice

By starting with small sets of zeros, you can develop an intuitive understanding of the process. Practicing polynomial factoring sharpens your algebraic skills, making you more efficient in writing polynomial functions.

Synthetic division streamlines the division process, saving you time and reducing the likelihood of errors. Utilizing additional resources allows you to explore different perspectives, reinforcing your knowledge base and fostering a deeper understanding of the topic.

Frequently Asked Questions

Q1: How do I find the zeros of a polynomial function?
A1: Use methods such as factoring, synthetic division, or numerical techniques like the Rational Root Theorem.

Q2: Can I write a polynomial function with any number of zeros?
A2: Yes, you can write a polynomial function with any finite number of zeros, including complex zeros.

Q3: What applications do polynomial functions have in real-world scenarios?
A3: Polynomial functions find applications in fields such as motion modeling, projectile trajectories, circuit analysis, and economic forecasting.

Conclusion

Understanding how to write polynomial functions with given zeros is a cornerstone of algebra. By embracing the Factor Theorem and following the steps outlined in this article, you can master this technique and expand your mathematical toolbox. Whether you’re a student, professional, or simply curious about mathematics, delving into the world of polynomial functions promises both intellectual stimulation and practical value.

Call to Action

Are you intrigued by the fascinating realm of polynomial functions? Embark on a deeper exploration by practicing writing functions with various sets of zeros. Share your experiences and ask questions in the comments section below, and let’s continue the mathematical journey together!

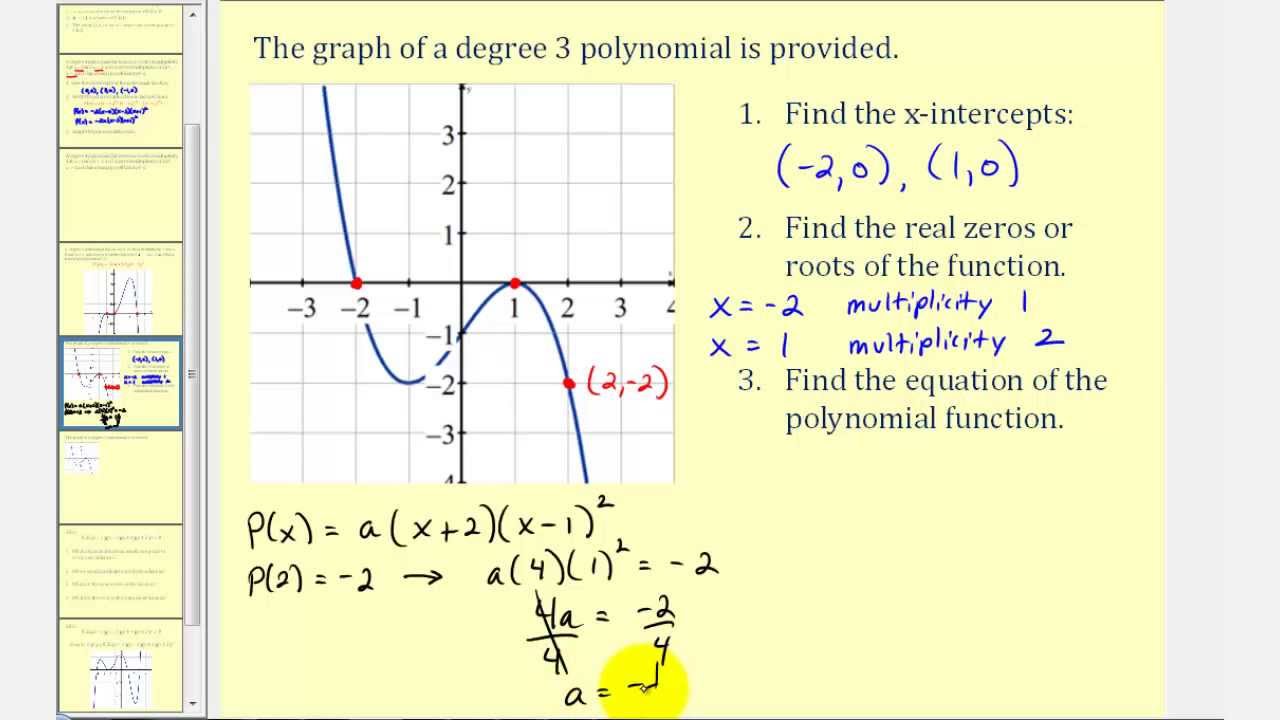
Image: kaylynafefisher.blogspot.com

Thank you for reading How To Write A Polynomial Function With Given Zeros on our site. We hope you find this article beneficial.